今天要介紹和 Dynamic Programming 有點相似的 Greedy。

Greedy 的核心概念很簡單：選擇你覺得最好的方案就對了。這個選擇的過程是單向的，今天遇到了第一個分岔點，你選擇了道路 A，那就必須一直走下去直到終點，不能中途覺得不對，又想回過來換成道路 B。而且，這種方法不會去評估 A、B、C 三條路，再看看確定要走哪條，是直接做出決定，然後在這個決定的基礎上再去做下一個決定。

要使用 Greedy 的條件和 Dynamic Programming 蠻類似的，就是問題的最佳解也會包含子問題的最佳解。在這個情況下，我們才可以一條路走到黑，並確保只要每個選擇點的決定都是最好的，就會得到最完美的結果。當然，條件不成立也是可以使用啦，但得到的就可能是近似解而不是最佳解了。

舉個實際的例子，假設今天要買東西，要怎麼達到效益最大化呢？當然是買你覺得 CP 值最高的東西了。於是我們可以列出一個物品清單，把 價值 / 價格 = CP 值，優先選擇 CP 值最高的東西，如果選完後還有剩下的錢，再買 CP 值第二高的東西，這樣買到沒錢為止，聽起來不難吧。

這就是有名的背包問題(Knapsack Problem)，目的是要在有限的空間中，裝進價值最多的物品。背包問題又有很多種變形題，像是每種物品只能挑 0 或 1 個，或是可以切成非整數個帶走，又或者每種物品最多可帶走的數量都不一樣、有各自的限制，大家有興趣的可以搜尋看看。

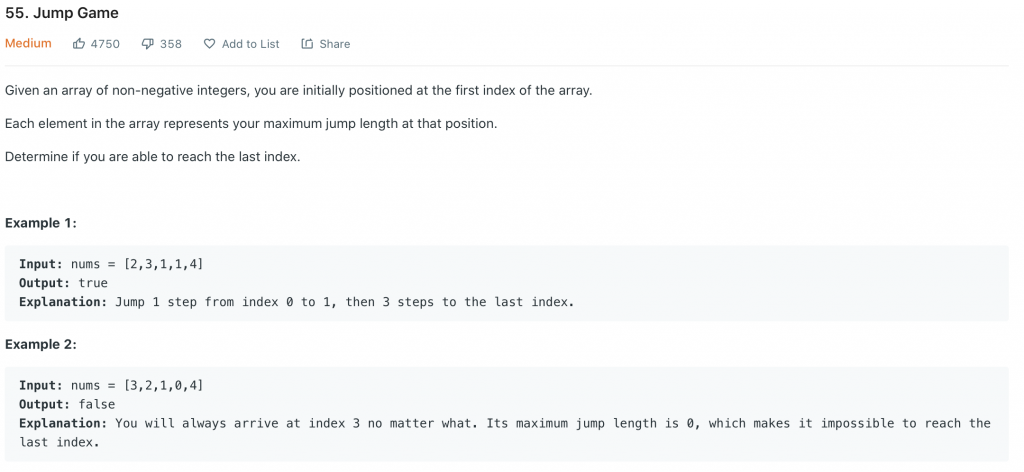
今天的問題跟昨天有點像，可以想像成跳樓梯問題。每個台階最多可以跳的階數都有規定，假如限制是 3，那走 1、2、3 階都可以。這個問題是要去判斷，在給定的限制下，有沒有辦法走到最後一階。

這個問題可以反推來解，假設今天可以從 n-1 走到 n 階，問題就縮小成第 1 階能不能跳到倒數第 n 階。n-1 到 n 階是否能到是很好判斷的，所以我們就能一路往回推到起點求答案。

// javascript
var canJump = function(nums) {
    let position = nums.length - 1
    for (let i = nums.length - 1; i >= 0; i--) {
      if (i + nums[i] >= position) {
        position = i
      }
    }
    return position == 0
};

// C++
class Solution {
public:
    bool canJump(vector<int>& nums) {
      int position(nums.size() - 1);
      for(int i = nums.size() - 1; i >= 0; i--)
        if (i + nums[i] >= position) {
          position = i;
        }
      return position == 0;
    }
};

最後順帶一提，不同語言的執行效率差距蠻驚人的，這邊提供上面兩個解法的執行結果給大家看看。實際原因就暫時略過，之後有空再來研究。

| |Runtime|Memory|
|javascript|68 ms|12.8 MB|
|C++ |16 ms|38 MB|

以上，文章有任何問題或錯誤都歡迎留言，感謝閱讀～